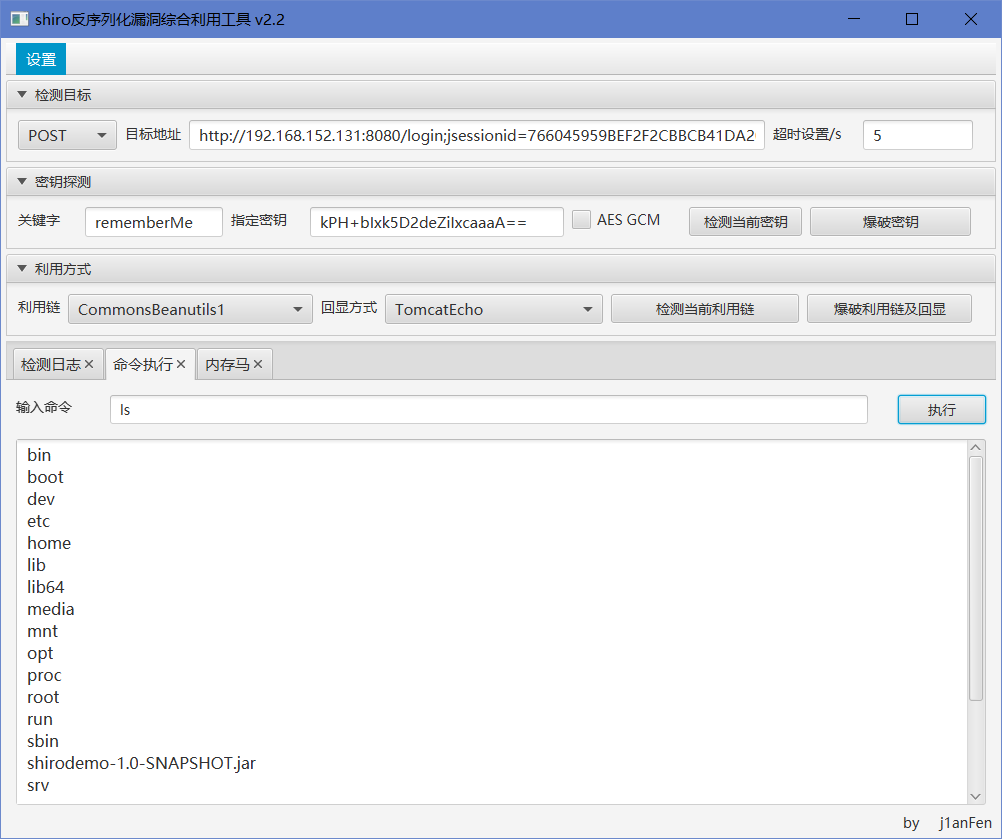
Shiro-721漏洞分析与复现
在上一篇文章中,我们分析了shiro 550的反序列化漏洞的原理以及应用,这次分析另一个shiro的高危漏洞shiro 721
shiro 721与550区别较大的是,550因为密钥为固定常量,导致可以伪造各种信息,而721修复了这一点,却又出现了新的问题
在shiro 721中,RememberMe Cookie 默认通过AES-128-CBC加密,而这种加密模式容易受到长度扩展攻击(在这里具体为Padding Oracle Attack( Oracle 填充攻击 )),攻击者可以使用有效的 RememberMe Cookie 作为Paddding Oracle Attack 的前缀,然后精心构造RememberMe Cookie 来实施反序列化攻击
- 使用任意账户登陆目标网站,以获取一个合法的RememberMe Cookie
- 将获取的值作为POA的前缀
- 加密反序列化的payload来构造恶意RememberMe Cookie
- 将构造好的恶意数据填充到 RememberMe Cookie字段中并发送
影响版本 1.2.5 <= Shiro <= 1.4.1
漏洞分析
首先,我们先得明确一点,这个漏洞能够被利用的核心,就是利用Padding Oracle Attack,那就先来分析下填充攻击
Padding Oracle Attack
AES-128-CBC加密,很好理解,使用的是AES加密算法,128bit为一个分组,而CBC指的是利用CBC加密模式
AES-128-CBC
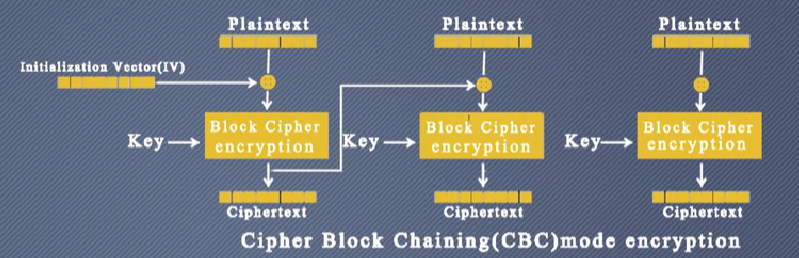
CBC 加密模式:将明文切分成若干小段,然后每一段分别与上一段的密文进行异或运算,再与密钥进行加密,生成本段明文的密文,这段密文用于下一段明文的加密。第一段明文没有对应的密文,为了确保分组的唯一性,CBC加密模式使用了初始化向量(IV,Initialization Vector)。初始化向量是一个固定长度的随机数,该向量会作为密文第一个块,随密文一同传输,在CBC模式中,因为链接模式中的异或操作是等长操作,所以初始化向量(IV)的长度与分组大小相同,为16 Bytes(128 bits)
纯粹的文字还是比较抽象,这里放上一张CBC加密的流程图,就很好理解了
首先把明文按照128bit为一组分组,再由初始化的向量IV与明文的第一组进行异或,加密,得到密文的第一组。再用刚得到的异地组密文与第二组明文异或,加密,得到密文的第二组依次往后
这样就很好理解了,但我们也会发现一个问题,在给明文分组的时候,如果不是128bit的倍数,也就是最后一组不够128bit(16byte)的时候怎么办,例如:
0123456789ABCDEF FEDCBA9876543210
这一共是32byte,也就是256bit刚好可以分为两组
0123456789ABCDEF FEDCBA987654
这一共是28byte, 也就是224bit,第二组不满128bit
如果就这样进入CBC中加密,那么在异或这一步的时候,就会因为位数不同而无法进行下去,故当初的算法设计这就想到了,使用PKCS5进行长度填充,比如在第二个例子中,最后缺少4个byte,则填充4个0x04,若缺少15个byte,则填充15个0x0f
填充Oracle攻击
Padding Oracle填充攻击(Padding Oracle Attack)是比较早的一种漏洞利用方式了,早在2011年的Pwnie Rewards中被评为“最具有价值的服务器漏洞”。这个漏洞主要是由于设计使用的场景不当,导致可以利用密码算法通过“旁路攻击”被破解。值得强调的是,这个漏洞启示并不是对算法本身的破解,而是利用算法本身的某些padding特性以及系统中不必要的一些错误提示,进而分析出系统当前的漏洞利用路径。同时也需要强调下,这里的Oracle,其实与甲骨文公司关系并不大,这里的Oracle可以理解为“提示、暗示”的含义。
既然是服务器漏洞,那么肯定会涉及到与服务器进行的交互,而这里就是用到服务器给出的回显或者相应的不同,来判断填充的是否正确,例如:
服务器返回200 -> 密文与填充均正确
服务器返回301 -> 密文正确,填充错误
服务器返回500 -> 密文与填充均错误
这里根据服务器的相应变化,穷举填充的值,其实很类似于SQL中的盲注
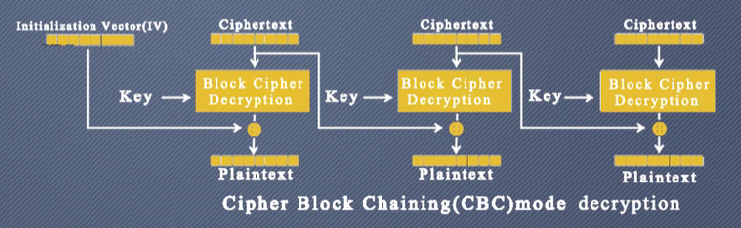
我们再来具体看CBC的解密流程
解密时,与加密一样,先将密文按128bit分组,然后将第一组密文与密钥进行解密,再与初始向量IV异或,得到第一组明文,第二组密文与密钥进行解密,再与第一组密文异或,得到第二组密文,以此进行解密
因为Oracle的任务是提交数据让服务器解密,并验证解密后明文分组是否正确,所以我们不需要去解密明文,那我们只需要去遍历输入的值,根据服务器的返回信息,来判断正确,知道我们找到正确的值,也就这个padding符合规范
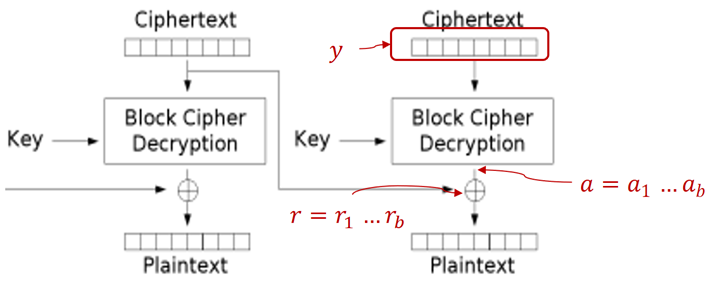
- 对于r的破解
根据CBC解密的流程,从最后一个分组入手,穷举猜测r使其满足CBC最后一个或者多个分组的输出填充规则,例如最后一个字节满足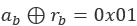
1
2
3
4
5
6
7
8
9
10
11
12
13
14for i in list:
for _ in list:
c2=c2[:30]+i+_
# c1=c1[:30]+i+_
# iv=iv[:30]+i+_
iv_c=iv+c1+c2+c3
# iv_c=iv+c1+c2
# iv_c=iv+c1
output = subp.call(['./dec_oracle.exe',iv_c])
if output==200:
print(i+_,'`````````````````````````') - 进一步判断填充的长度
接下来就是进一步判断填充的长度,从r1入手,逐个字修改与确认1
2
3
4
5
6
7
8
9
10
11
12for i in range(0,32,2):
r=r1[:i]+'00'+r1[i+2:]
iv_c_new=iv+c1+r+c3
# iv_c_new=iv+r+c2
#iv_c_new=r+c1
output = subp.call(['./dec_oracle.exe',iv_c_new])
if output==500:
len=16-i/2
print(len) #填充长度len=1,第二组填充长度len=1,第三组填充长度len=1
print(hex(0x01^0x3d)) - 进一步得到aj-1
通过调整r,将CBC解密后的填充修改为长度为b-j+2的形式,即让aj-1对应的字节也成为填充1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23for n in range(1,16):
for i in list:
for _ in list:
r1=r1[:30-n*2]+i+_+r1[32-n*2:]
iv_c_new=iv+c1+r1+c3
# iv_c_new=iv+r1+c2
# iv_c_new=r1+c1
output = subp.call(['./dec_oracle.exe',iv_c_new])
if output==200:
print(i+_,'``````````````````````````````````succeed!````````````````````````````````````')
num=(int(i+_,16)^(n+1))
num=hex(num)
if(len(num)<4):
num='0x0'+num[2:]
a.insert(0,num[2:])
break
r1=r1[:32-(n+1)*2]
for q in range(n+1):
if(len(hex(int(a[q],16)^(n+2)))<4):
r1+='0'
r1+=(hex(int(a[q],16)^(n+2))[2:]) - 得到其他分组
利用上述方法可以恢复任意一个分组,的解密中间状态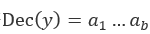
此时再根据截获的上一个分组密文y’,来获得真实的明文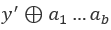
在不知道密钥的情况下,完成数据的加密,绕过服务端的校验(解密成功+明文有效),达到攻击的目的,这就是填充Oracle攻击
漏洞利用
可以下载p神的环境
换一下pom.xml中shiro的版本即可
然后有exp也可以直接使用exp
我这里还是为了省事,直接用vulhub搭建的
然后还是工具一把梭